Xác định tâm mặt cầu ngoại tiếp hình chóp

Bài viết hướng dẫn phương pháp xác định trung khu và nửa đường kính mặt ước ngoại tiếp hình chóp, kỹ năng và kiến thức và những ví dụ trong nội dung bài viết được xem thêm từ các tài liệu nón – trụ – cầu đăng cài trên hydroxyzinex.com.

Bạn đang xem: Xác định tâm mặt cầu ngoại tiếp hình chóp

Phương pháp: Cách xác định tâm và nửa đường kính mặt cầu ngoại tiếp hình chóp: + khẳng định trục $d$ của con đường tròn ngoại tiếp nhiều giác đáy ($d$ là con đường thẳng vuông góc với đáy tại trung tâm đường tròn ngoại tiếp nhiều giác đáy). + khẳng định mặt phẳng trung trực $left( p. Right)$ của một kề bên (hoặc trục $Delta $ của của con đường tròn nước ngoài tiếp một nhiều giác của phương diện bên). + Giao điểm $I$ của $left( p. Right)$ và $d$ (hoặc của $Delta $ và $d$) là trọng điểm mặt mong ngoại tiếp hình chóp. + nửa đường kính của mặt ước ngoại tiếp hình chóp là độ nhiều năm đoạn thẳng nối chổ chính giữa $I$ với một đỉnh của hình chóp.

Bạn vẫn xem: xác minh tâm và bán kính mặt ước ngoại tiếp hình chóp

Nhận xét: Hình chóp gồm đáy hoặc những mặt mặt là những đa giác không nội tiếp được mặt đường tròn thì hình chóp đó không nội tiếp được khía cạnh cầu.

Ta xét một số dạng hình chóp thường gặp và cách xác định tâm và nửa đường kính mặt cầu ngoại tiếp hình chóp đó. Dạng 1. Hình chóp có các điểm cùng quan sát một đoạn trực tiếp $AB$ bên dưới một góc vuông. Phương pháp: + Tâm: Trung điểm của đoạn thẳng $AB$. + cung cấp kính: $R=fracAB2$.

Ví dụ: • Hình chóp $S.ABC$ tất cả đường cao $SA$, lòng $ABC$ là tam giác vuông tại $B.$

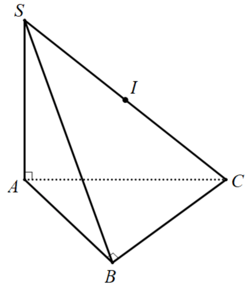
Ta gồm $widehat SAC = widehat SBC = 90^o$, suy ra $A,B$ cùng chú ý $SC$ dưới một góc vuông. Lúc đó, mặt cầu ngoại tiếp hình chóp $S.ABC$ có: + chổ chính giữa $I$ là trung điểm của $SC.$ + chào bán kính: $R = fracSC2.$

• Hình chóp $S.ABCD$ có đường cao $SA$, đáy $ABCD$ là hình chữ nhật.

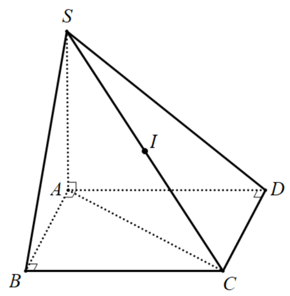
Ta có $widehat SAC = widehat SBC = widehat SDC = 90^o$, suy ra $A,B,D$ cùng quan sát $SC$ dưới một góc vuông. Lúc đó, mặt mong ngoại tiếp hình chóp $S.ABCD$ có: + trung khu $I$ là trung điểm của $SC.$ + chào bán kính: $R = fracSC2.$

Ví dụ 1: mang đến hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông trên $B$, $SA$ vuông góc với phương diện phẳng $left( ABC right)$ cùng $SC=2a$. Tính bán kính mặt ước ngoại tiếp hình chóp $S.ABC$.

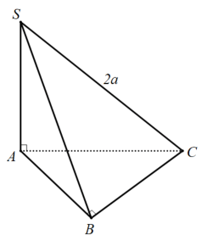
Ta có: $left{ beginarrayl BC bot AB BC bot SA left( SA bot left( ABC right) right) endarray right.$ $ Rightarrow BC bot left( SAB right)$ $ Rightarrow BC bot SB.$ $SA bot left( ABC right)$ $ Rightarrow SA bot AC.$ Suy ra: nhị điểm $A$, $B$ cùng nhìn $SC$ bên dưới một góc vuông. Vậy nửa đường kính mặt mong ngoại tiếp hình chóp $S.ABC$ là: $R = fracSC2 = a.$

Ví dụ 2: cho hình chóp $S.ABCD$ có đáy $ABCD$là hình vuông tại, $SA$ vuông góc với phương diện phẳng $left( ABCD right)$ cùng $SC=2a$. Tính bán kính mặt mong ngoại tiếp hình chóp $S.ABCD$.

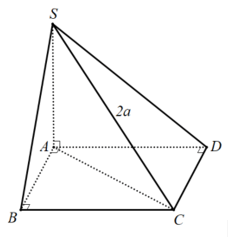
Ta có: $left{ beginarrayl BC bot AB BC bot SA endarray right.$ $ Rightarrow BC bot left( SAB right)$ $ Rightarrow BC bot SB.$ chứng tỏ tương từ bỏ ta được: $CD bot SD.$ $SA bot left( ABCD right)$ $ Rightarrow SA bot AC.$ Suy ra: cha điểm $A$, $B$, $D$ cùng chú ý $SC$ dưới một góc vuông. Vậy nửa đường kính mặt mong là $R=fracSC2=a.$

Dạng 2. Hình chóp đều. Phương pháp: • Hình chóp tam giác hầu hết $S.ABC$:

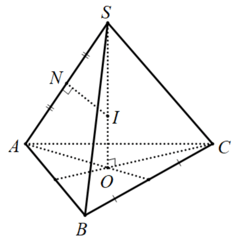
• Hình chóp tứ giác những $S.ABCD$:

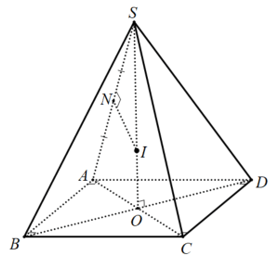
Gọi $O$ là tâm của đáy $Rightarrow SO$ là trục của đường tròn nước ngoài tiếp đa giác đáy. Trong mặt phẳng xác định bởi $SO$ và một cạnh bên, chẳng hạn như $textmpleft( SAO right)$, ta vẽ đường trung trực của cạnh $SA$ và cắt $SO$ tại $I$ $Rightarrow I$ là trung tâm của mặt cầu ngoại tiếp hình chóp. Ta có: $Delta SNI ∼ Delta SOA$ $ Rightarrow fracSNSO = fracSISA$, suy ra bán kính mặt cầu ngoại tiếp hình chóp là: $R = IS = fracSN.SASO = fracSA^22SO.$

Ví dụ 3: Tính nửa đường kính của mặt mong ngoại tiếp hình chóp tam giác đông đảo $S.ABC$, biết những cạnh đáy tất cả độ dài bằng $a$, cạnh bên $SA=asqrt3$.

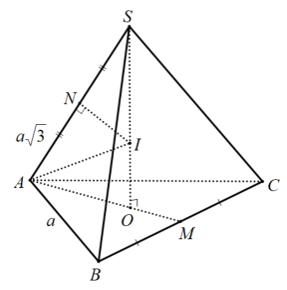
Gọi $O$ là vai trung phong của tam giác mọi $ABC$, ta tất cả $SObot left( ABC right)$ đề nghị $SO$ là trục của đường tròn ngoại tiếp tam giác $ABC$. điện thoại tư vấn $N$ là trung điểm của $SA$, vào $mpleft( SAO right)$ kẻ trung trực của $SA$ cắt $SO$ trên $I$ thì $IS$ = $IA$ = $IB$ = $IC$ cần $I$ đó là tâm mặt cầu ngoại tiếp hình chóp $S.ABC$. Nửa đường kính mặt mong là $R=SI$. Vày hai tam giác $SNI$ cùng $SOA$ đồng dạng phải ta tất cả $fracSNSO=fracSISA$. Suy ra $R=SI=fracSN.SASO$ $=fracSA^22SO=frac3asqrt68$. Mà $AO=frac23fracasqrt32=fracasqrt33$, $SO=sqrtSA^2-AO^2=frac2asqrt63$. Nên $R=SI=frac3asqrt68$.

Xem thêm: Nơi Bán Card Màn Hình 1Gb Cao Cấp, Sale Sốc, Với Nhiều Ưu Đãi

Ví dụ 4: Tính bán kính của mặt ước ngoại tiếp hình chóp tứ giác đều phải có cạnh đáy bởi $a$, sát bên bằng $2a$.

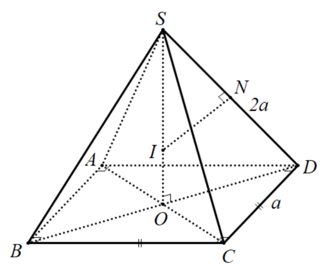
Gọi $O$ là trọng tâm đáy thì $SO$ là trục của hình vuông vắn $ABCD$. điện thoại tư vấn $N$ là trung điểm của $SD$, trong $mp(SDO)$ kẻ trung trực của đoạn $SD$ cắt $SO$ tại $I$ thì $IS = IA = IB = IC = ID$ đề xuất $I$ là tâm của mặt ước ngoại tiếp hình chóp $S.ABCD$. Bán kính mặt mong là $R=SI$. Ta có: $Delta SNI ∼ Delta SOD$ $ Rightarrow fracSNSO = fracSISD$ $ Rightarrow R = ham = fracSD.SNSO = fracSD^22SO.$ mà $SO^2 = SD^2 – OD^2$ $ = 4a^2 – fraca^22 = frac7a^22$ $ Rightarrow SO = fracasqrt 7 sqrt 2 .$ Vậy $R = fracSD^22SO = frac2asqrt 14 7.$

Dạng 3. Hình chóp có sát bên vuông góc với khía cạnh phẳng đáy. Phương pháp: mang đến hình chóp $S.A_1A_2…A_n$ có cạnh mặt $SAbot left( A_1A_2…A_n right)$ và đáy $A_1A_2…A_n$ nội tiếp được trong đường tròn trọng tâm $O$. Trung tâm và bán kính mặt cầu ngoại tiếp hình chóp $S.A_1A_2…A_n$ được xác định như sau: + Từ trọng tâm $O$ ngoại tiếp của đường tròn đáy, ta vẽ đường thẳng $d$ vuông góc với $mpleft( A_1A_2…A_n right)$ tại $O$. + vào $mpleft( d,SA_1 right)$, ta dựng đường trung trực $Delta $ của cạnh $SA$, cắt $SA_1$ tại $N$, cắt $d$ tại $I$. + khi đó: $I$ là trung tâm mặt cầu ngoại tiếp hình chóp, bán kính $R=IA_1=IA_2=…=IA_n=IS$. + Tìm bán kính: Ta có: $MIOA_1$ là hình chữ nhật, xét $Delta MA_1I$ vuông tại $M$ có: $R = A_1I = sqrt MI^2 + MA_1^2 $ $ = sqrt A_1O^2 + left( fracSA_12 right)^2 .$

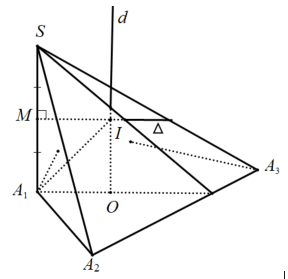
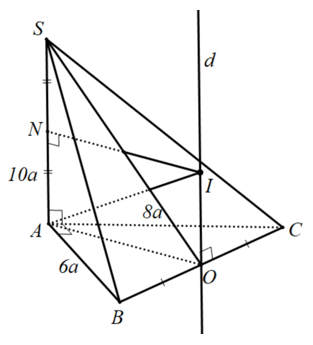
Ví dụ 5: cho hình chóp $S.ABC$ có cạnh $SA$ vuông góc với đáy, $ABC$ là tam giác vuông tại $A$, biết $AB=6a$, $AC=8a$, $SA=10a$. Tìm bán kính của mặt mong ngoại tiếp hình chóp $S.ABC$.

Tham khảo: kỹ năng Ngăn vật liệu bằng nhựa tủ giá bị gãy – phương pháp thay thế

Gọi $O$ là trung điểm của cạnh $BC$. Suy ra $O$ là trọng điểm đường tròn ngoại tiếp tam giác $ABC$ vuông trên $A$. Dựng trục $d$ của đường tròn ngoại tiếp tam giác $ABC$; trong mặt phẳng $left( SA,d right)$ vẽ trung trực cạnh $SA$ và cắt $d$ trên $I$. Suy ra $I$ là tâm mặt mong ngoại tiếp hình chóp $S.ABC$ và bán kính $R=IA=IB=IC=IS$. Ta tất cả tứ giác $NIOA$ là hình chữ nhật. Xét tam giác $NAI$ vuông tại $N$ có: $R = IA = sqrt NI^2 + NA^2 $ $ = sqrt AO^2 + left( fracSA2 right)^2 $ $ = sqrt left( fracBC2 right)^2 + left( fracSA2 right)^2 $ $ = sqrt fracAB^2 + AC^24 + left( fracSA2 right)^2 $ $ = 5asqrt 2 .$

Ví dụ 6: mang đến hình chóp $S.ABC$ gồm cạnh $SA$ vuông góc với đáy, $ABC$ là tam giác đều cạnh bởi $a$, $SA=2a$. Tìm nửa đường kính của mặt mong ngoại tiếp hình chóp $S.ABC$.

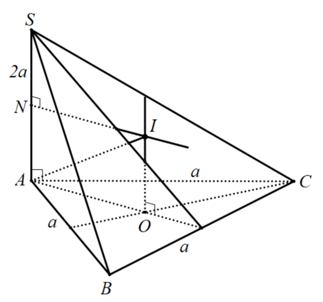
Gọi $O$ là giữa trung tâm của tam giác $ABC$. Suy ra $O$ là trung tâm đường tròn nước ngoài tiếp tam giác đều $ABC$. Dựng trục $d$ của mặt đường tròn ngoại tiếp tam giác $ABC$; trong khía cạnh phẳng $left( SA,d right)$ vẽ trung trực cạnh $SA$ và cắt $d$ trên $I$. Suy ra $I$ là trung tâm mặt mong ngoại tiếp hình chóp $S.ABC$ và nửa đường kính $R=IA=IB=IC=IS$. Ta bao gồm tứ giác $NIOA$ là hình chữ nhật. Xét tam giác $NAI$ vuông trên $N$ có: $R = IA = sqrt NI^2 + NA^2 $ $ = sqrt AO^2 + left( fracSA2 right)^2 $ $ = sqrt left( frac23 cdot fracasqrt 3 2 right)^2 + left( frac2a2 right)^2 $ $ = frac2asqrt 3 3.$

Ví dụ 7: mang đến hình chóp $S.ABC$ bao gồm cạnh $SA$ vuông góc với đáy, $ABC$ là tam giác cân tại $A$ và $AB=a$, $widehatBAC=120^o $, $SA=2a$. Tính nửa đường kính của mặt ước ngoại tiếp hình chóp $S.ABC$.

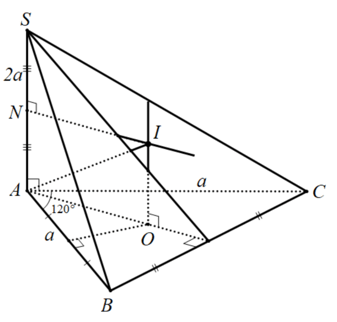
Gọi $O$ là vai trung phong đường tròn ngoại tiếp của tam giác $ABC$. Dựng trục $d$ của mặt đường tròn nước ngoài tiếp tam giác $ABC$; trong mặt phẳng $left( SA,d right)$ vẽ trung trực cạnh $SA$ và cắt $d$ tại $I$. Suy ra $I$ là trung ương mặt cầu ngoại tiếp hình chóp $S.ABC$ và nửa đường kính $R=IA=IB=IC=IS$. Mặt khác, ta có: $S_ABC = frac12AB.AC.sin A$ $ = fraca^2sqrt 3 4$ cùng $BC = sqrt AB^2 + AC^2 – hydroxyzinex.com.cos rmA $ $ = asqrt 3 .$ $OA$ là bán kính đường tròn nước ngoài tiếp tam giác $ABC$ buộc phải $OA = fracAB.BC.CA4S_ABC = a.$ Tứ giác $NIOA$ là hình chữ nhật buộc phải $NI=OA=a$. Xét tam giác $NAI$ vuông tại $N$ có: $R = IA = sqrt NI^2 + NA^2 $ $ = sqrt AO^2 + left( fracSA2 right)^2 $ $ = sqrt a^2 + a^2 = asqrt 2 .$

Dạng 4. Hình chóp xuất hiện bên vuông góc với phương diện phẳng đáy. Đối với dạng toán này thì mặt bên vuông góc hay là tam giác vuông, tam giác cân hoặc tam giác đều. Phương pháp: + xác định trục $d$ của con đường tròn đáy. + xác minh trục $Delta $ của đường tròn nước ngoài tiếp mặt bên vuông góc cùng với đáy. + Giao điểm $I$ của $d$ và $Delta $ là trung tâm mặt cầu ngoại tiếp hình chóp.

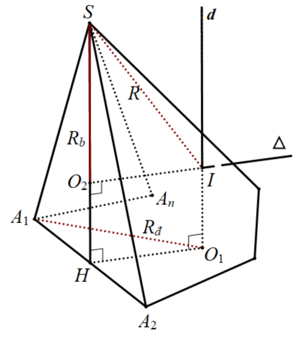
Xét hình chóp $S.A_1A_2cdots A_n$ xuất hiện bên vuông góc với khía cạnh đáy, ko mất tính quát mắng ta mang sử mặt bên $left( SA_1A_2 right)$ vuông góc với dưới mặt đáy và $Delta SA_1A_2$ là tam giác vuông hoặc tam giác cân nặng hoặc tam giác đều. Hotline $O_1$ cùng $O_2$ lần lượt là tâm đường tròn nước ngoài tiếp đa giác $A_1A_2cdots A_n$ cùng tam giác $SA_1A_2$. Dựng $d$ cùng $Delta $ theo thứ tự là trục con đường tròn ngoại tiếp đa giác $A_1A_2cdots A_n$ và tam giác $SA_1A_2$. Hotline $I$ là giao điểm của $d$ và $Delta $ thì $I$ cách đều những đỉnh $A_1$, $A_2$, …, $A_n$ cùng $S$ yêu cầu $I$ là trung ương mặt ước ngoại tiếp hình chóp $S.A_1A_2cdots A_n$. Ta gồm tứ giác $O_2IO_1H$ là hình chữ nhật; $SI=R$ là nửa đường kính mặt ước ngoại tiếp $S.A_1A_2cdots A_n$; $SO_2=R_b$ là nửa đường kính đường tròn nước ngoài tiếp tam giác $SA_1A_2$; $A_1O_1=R_đ$ là nửa đường kính đường tròn nước ngoài tiếp đa giác $A_1A_2cdots A_n$. Tam giác $SO_2I$ vuông trên $O_2$ nên: $SI = sqrt SO_2^2 + O_2I^2 $ $ = sqrt SO_2^2 + O_1H^2 .$ Tam giác $A_1O_1H$ vuông tại $H$ nên: $O_1H^2 = O_1A_1^2 – A_1H^2.$ do đó: $SI = sqrt SO_2^2 + O_1A_1^2 – A_1H^2 .$ khía cạnh khác, nếu tam giác $SA_1A_2$ vuông trên $S$ thì $O_2equiv H$ cùng trùng cùng với trung điểm $A_1A_2$ hoặc $SA_1A_2$ là tam giác cân nặng tại $S$ hoặc số đông thì ta cũng có thể có $H$ trùng cùng với trung điểm $A_1A_2$ nên $A_1H=fracA_1A_22$. Suy ra $SI = sqrt SO_2^2 + O_1A_1^2 – left( fracA_1A_22 right)^2 .$ giỏi $R = sqrt R_b^2 + R_đ^2 – fracpartial ^24 $, cùng với $partial $ là độ nhiều năm cạnh cạnh bình thường của mặt mặt vuông góc với đáy.

Ví dụ 8: mang đến hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông cân nặng tại $A$. Mặt bên $left( SAB right)bot left( ABC right)$ với $Delta SAB$ đông đảo cạnh bằng $1$. Tính nửa đường kính mặt ước ngoại tiếp hình chóp $S.ABC$.

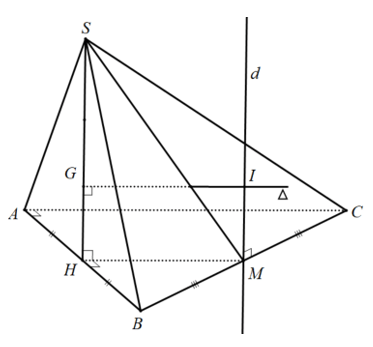
Gọi $H$, $M$ theo lần lượt là trung điểm của $AB$, $AC$. Ta tất cả $M$ là trọng điểm đường tròn nước ngoài tiếp $Delta ABC$ (do $MA=MB=MC$). Dựng $d$ là trục mặt đường tròn ngoại tiếp $Delta ABC$ ($d$ qua $M$ và song song $SH$). Hotline $G$ là trọng tâm đường tròn ngoại tiếp $Delta SAB$ cùng $Delta $ là trục mặt đường tròn ngoại tiếp $Delta SAB$, $Delta $ giảm $d$ trên $I$. Suy ra $I$ là vai trung phong mặt ước ngoại tiếp hình chóp $S.ABC$. Suy ra nửa đường kính $R=SI$. Xét $Delta SGI$, suy ra $SI=sqrtGI^2+SG^2$. Nhưng $SG=frac1sqrt3$; $GI=HM=frac12AC=frac12$. đề xuất $R=SI=sqrtfrac13+frac14=fracsqrt216$.

Ví dụ 9: đến hình chóp $S.ABC$ tất cả đáy $ABC$ là tam giác đều cạnh bởi $1$, mặt mặt $SAB$ là tam giác hầu hết và bên trong mặt phẳng vuông góc với khía cạnh phẳng đáy. Tính thể tích $V$ của khối cầu ngoại tiếp hình chóp sẽ cho.

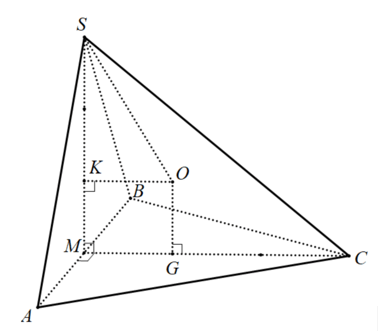
Gọi $M$ là trung điểm của $AB$ thì $SMbot AB$ (vì tam giác $SAB$ đều). Khía cạnh khác bởi $left( SAB right)bot (ABC)$ bắt buộc $SMbot (ABC)$. Tương tự: $CMbot (SAB)$. Gọi $G$ cùng $K$ theo thứ tự là tâm của những tam giác $ABC$ với $SAB$. Trong phương diện phẳng $(SMC)$, kẻ con đường thẳng $Gxtext//SM$ và kẻ mặt đường thẳng $Kybot SM$. Gọi $O=Gxcap Ky$, thì ta có: $left{ beginarrayl OG bot (SAB) OK bot (ABC) endarray right.$ Suy ra $OG,OK$ lần lượt là trục của tam giác $ABC$ cùng $SAB$. Cho nên vì thế ta có: $OA=OB=OC=OD=OS$ hay $O$ chính là tâm mặt cầu ngoại tiếp hình chóp $S.ABC$. Tứ giác $OKMN$ là hình chữ nhật bao gồm $MK=MG=fracsqrt36$ đề nghị $OKMN$ là hình vuông. Vì thế $OK=fracsqrt36$. Ngoài ra $SK=fracsqrt33$. Xét tam giác $SKO$ vuông trên $K$ tất cả $OS = sqrt OK^2 + SK^2 $ $ = sqrt frac336 + frac39 = fracsqrt 15 6.$ Suy ra bán kính mặt cầu buộc phải tìm là $R=OS=fracsqrt156$. Vậy thể tích khối cầu cần tìm là: $V = frac43pi R^3$ $ = frac43pi .left( fracsqrt 15 6 right)^3$ $ = frac5sqrt 15 pi 54.$