Tính chất ngũ giác đều
-
Hôm nay chúng ta sẽ chú ý một cáchdựng hìnhngũ giác đềubằng thước và compa phụ thuộc công thức lượng giác tiếp sau đây $$cosfracpi5 = frac1 + sqrt54.$$
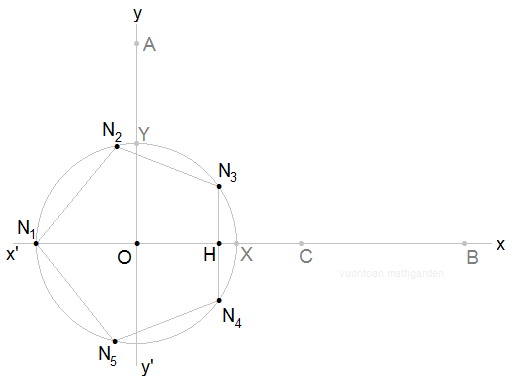
Vì $$angle N_3 O H = frac12 angle N_3 O N_4 = fracpi5$$ bắt buộc $$OH = r cosfracpi5$$ trong số ấy $r$ là bán kính của mặt đường tròn vai trung phong $O$.Vậy để dựng điểm $H$, chúng ta cần tính $cosfracpi5$.Tính $cosfracpi5$Góc $fracpi5$ bao gồm tính chất sau đây $$2 fracpi5 + 3 fracpi5 = pi$$ cho nên, nếu chúng ta đặt $x = fracpi5$ thì $2 x + 3 x =pi$, tức là $2x$ và $3x$ là hai góc bù nhau, và bọn họ suy ra $$cos2x = - cos3x.$$Áp dụng công thức lượng giác mang đến góc gấp hai và góc cấp ba bọn họ có $$cos2 x = 2 cos^2x - 1,$$ $$cos3 x = 4 cos^3x - 3 cosx,$$
Trở lại với hình vẽ trên $$OH = r cosfracpi5 = frac(1 + sqrt5) r4$$Để dựng được đoạn $OH$ thì bọn họ cần dựng đoạn thẳng bao gồm độ dài $(1 + sqrt5) r$ rồi phân chia nó ra có tác dụng 4 phần bởi nhau.Để dựng được đoạn thẳng bao gồm độ nhiều năm $(1 + sqrt5) r$ thì chúng ta cần dựng đoạn thẳng gồm độ lâu năm $sqrt5 r$.Nói mang đến số $sqrt5$, bọn họ sực lưu giữ ra định lý Pitagovì $5 = 1^2 + 2^2$.
Định lý Pitago nói rằng trong một tam giác vuông thì bình phương cạnh huyền bằng tổng bình phương của nhì cạnh góc vuông. Cho nên nếu chúng ta dựng một hình tam giác vuông gồm hai cạnh góc vuông là $r$ với $2r$ thì cạnh huyền sẽ bởi $sqrt5 r$
Bạn đang xem: Tính chất ngũ giác đều
Chúng ta có thể dễ dàng dựng được hình tam giác đều, hình vuông, hình lục giác hầu hết (6 cạnh) và hình chén bát giác đa số (8 cạnh). Vậy hình ngũ giác số đông (5 cạnh), hình thất giác đều (7 cạnh) cùng hình cửu giác các (9 cạnh) thì sao?Hoá ra, dùng thước với compa, bạn có thể dựng được hình ngũ giác đều. Mà lại thất giác phần đa và cửu giác hầu hết thì câu trả lời là ko thể! hôm nay chúng ta đã xem xét giải pháp dựng ngũ giác đều, còn thất giác những và cửu giác phần đông thì chúng ta để dành cho các kỳ sau.Bây giờ bọn họ hãy cùng phân tích. Ở hình mẫu vẽ sau đây, họ thấy rằng nếu chúng ta dựng đạt điểm $H$, thì tự điểm $H$, chúng ta có thể dựng được đỉnh $N_3$ với $N_4$, với từ đó họ dễ dàng dựng được hình ngũ giác đa số $N_1 N_2 N_3 N_4 N_5$.Vì $$angle N_3 O H = frac12 angle N_3 O N_4 = fracpi5$$ bắt buộc $$OH = r cosfracpi5$$ trong số ấy $r$ là bán kính của mặt đường tròn vai trung phong $O$.Vậy để dựng điểm $H$, chúng ta cần tính $cosfracpi5$.Tính $cosfracpi5$Góc $fracpi5$ bao gồm tính chất sau đây $$2 fracpi5 + 3 fracpi5 = pi$$ cho nên, nếu chúng ta đặt $x = fracpi5$ thì $2 x + 3 x =pi$, tức là $2x$ và $3x$ là hai góc bù nhau, và bọn họ suy ra $$cos2x = - cos3x.$$Áp dụng công thức lượng giác mang đến góc gấp hai và góc cấp ba bọn họ có $$cos2 x = 2 cos^2x - 1,$$ $$cos3 x = 4 cos^3x - 3 cosx,$$
Xem thêm: Cách Làm Thẻo Câu Cá Bông Lau (Bột), Nghề Qua Đêm Câu Cá Bông Lau
Trở lại với hình vẽ trên $$OH = r cosfracpi5 = frac(1 + sqrt5) r4$$Để dựng được đoạn $OH$ thì bọn họ cần dựng đoạn thẳng bao gồm độ dài $(1 + sqrt5) r$ rồi phân chia nó ra có tác dụng 4 phần bởi nhau.Để dựng được đoạn thẳng bao gồm độ nhiều năm $(1 + sqrt5) r$ thì chúng ta cần dựng đoạn thẳng gồm độ lâu năm $sqrt5 r$.Nói mang đến số $sqrt5$, bọn họ sực lưu giữ ra định lý Pitagovì $5 = 1^2 + 2^2$.
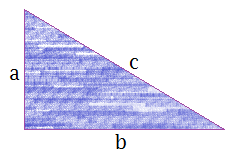 |
| Định lý Pitago: $c^2 = a^2+ b^2$. |
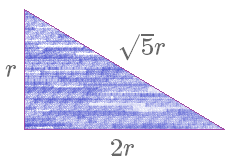 |
| $$(r)^2 + (2r)^2 = (sqrt5 r)^2$$ |











